Researchers at Institute of Modern Physics, Chinese Academy of Sciences (IMP), together with physicists from Tour University and Cambridge University, have explored separability and dynamical symmetry of Quantum Dots both in classical and quantum pictures.

The separability and Runge–Lenz-type dynamical symmetry of the internal dynamics of certain two-electron Quantum Dots, found by Simonović et al. (2003), are traced back to that of the perturbed Kepler problem. A large class of axially symmetric perturbing potentials made separation in parabolic coordinates found easily. Apart from the 2:1 anisotropic harmonic trapping potential considered in Simonović and Nazmitdinov (2013), they included a constant electric field parallel to the magnetic field (Stark effect), the ring-shaped Hartmann potential, etc. The harmonic case was studied in details.

Researchers at IMP claimed that the Quantum Dots system has a conserved Runge–Lenz type quantity, and the separability of quantum dots is derived from that of the perturbed Kepler problem. Moreover, harmonic perturbation with 2:1 anisotropy is separable in parabolic coordinates. The classical and quantum solutions of Quantum Dots are shown in Fig.1 and Fig.2. Researchers also mentioned that their problem can further be generalized by including magnetic charges.   

The work has been published in: Annals of Physics 341 (2014) 94–116 

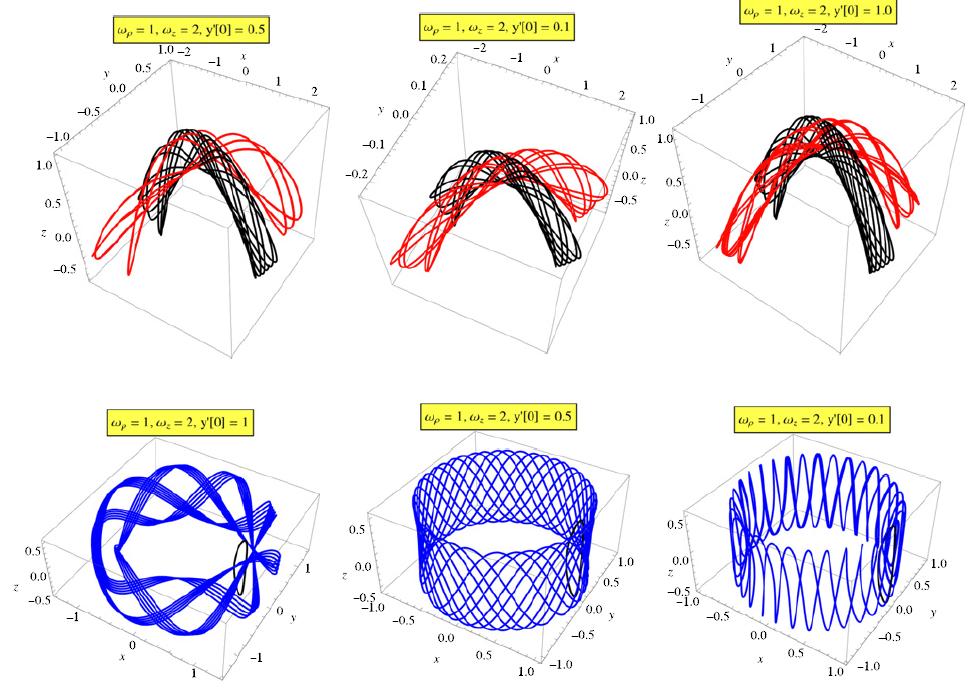
Fig1. Some 3D trajectories in the repulsive Coulomb potential with different parameters in Quantum Dots system (Image by IMP) 

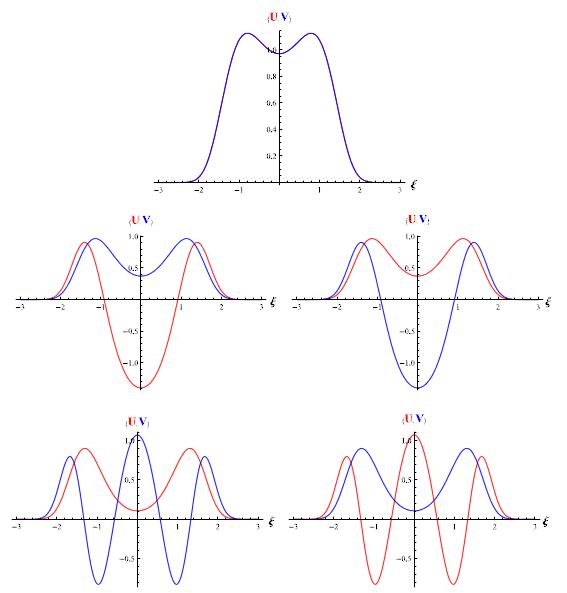
Fig 2. The lowest-energy states for the 2:1 oscillator coupled to a repulsive Coulomb potential, relevant for Quantum Dots (Image by IMP)